文献情報
- タイトル: Assessment of image generation by quantum annealer
- 著者: Takehito Sato, Masayuki Ohzeki, and Kazuyuki Tanaka
- 書誌情報: Sci Rep 11, 13523 (2021). https://doi.org/10.1038/s41598-021-92295-9
概要
量子アニーリングは組み合わせ最適化問題の求解に用いられることが多い一方で、画像生成を始めとした生成モデルにアニーリングを用いる手法も提案されています。
本論文では、ボルツマンマシンの学習内のサンプリングにD-Waveマシンを用いることで、その画像生成の品質向上を目的としています。
先行研究ではボルツマンマシンの評価指標の1つであるカルバック・ライブラー情報量という指標が、D-Waveマシンを用いることで小さくなったことが確認されていました。
しかし、それは確かに分布の近さを測ることはできますが、画像自体の品質を測ることはできません。
そこで、本論文では分類器としてニューラルネットワークを予め学習しておき、特定の数字の画像を生成したときに、その画像の分類結果を測ることで直接的な評価を可能にしています。
また、量子アニーリングを用いた手法が古典手法に対し、評価指標や過学習の有無において優位性を持つことも示します。
背景・課題
ボルツマシン
ボルツマンマシンは無向グラフに対応した確率モデルで、各ノードの状態$x_i$を確率変数とみなしたとき、グラフに$M$個あるノードすべての状態を$\textbf{x} = [x_1, …, x_M]$とすると以下の確率分布で表します。
\begin{align}
p(\textbf{x} | \theta) = \frac{1}{Z(\theta)} \exp(-\Phi(\textbf{x}, \theta))
\end{align}
ただし、$\Phi(\textbf{x}, \theta)$はエネルギー関数と呼ばれ、以下のように表します。
\begin{align}
\Phi = -\sum_{i=1}^{M} b_i x_i – \sum_{\{i, j\} \in E}w_{ij} x_i x_j
\end{align}
ここで、$E$はエッジの集合です。
また、$\theta$は式内の$b_i$、$w_{ij}$に対応しており、それぞれバイアス、重みと呼びます。
次に、$p(x | \theta)$式内の$Z(\theta)$は規格化定数で、分配関数とも呼ばれ、以下のように表されます。
\begin{align}
Z(\theta) = \sum_{\textbf{x}} \exp(-\Phi(\textbf{x}, \theta))
\end{align}
ここで、和$\sum_{\textbf{x}}$は、
\begin{align}
\sum_{\textbf{x}} = \sum_{x_1=0, 1} \sum_{x_2=0, 1} \cdots \sum_{x_M=0, 1}
\end{align}
のように、ボルツマンマシンの状態$\textbf{x}$のすべての値の組み合わせについての和で表されます。各状態が{0, 1}の2値を取るため、その組み合わせは$2^M$通りです。
次に、ボルツマンマシンの学習、つまりモデル分布$p(x|\theta)$が真の分布$p_g(x)$に最も近くなるようにモデルのパラメータ$\theta$を更新しなくてはいけません。
この分布の近さを表す尺度として、カルバック・ライブラー(KL)情報量が用いられます。上の2つの確率分布を用いると、KL情報量は以下の様になります。
\begin{align}
D_{KL}(p_g(x)||p(x|\theta)) = \sum_{n=1}^{N}p_g(\textbf{x}_n)\log{p_g(\textbf{x}_n)} – \sum_{n=1}^{N}p_g(\textbf{x}_n)\log{p(\textbf{x}_n|\theta)}
\end{align}
ここで、第2項は$E_{p_g(\textbf{x})}[\log{p(\textbf{x} | \theta)}]$と期待値の形で表せるため、その期待値を訓練データ$\mathcal{D} = [\textbf{x}_1, \dots, x_{N}]$での平均値で近似すると、以下のように表せます。
\begin{align}
E_{p_g(\textbf{x})}[\log p(\textbf{x} | \theta)]
&\approx \frac{1}{N}\log \prod_{n=1}^{N}p(\textbf{x}_n|\theta) \\
&= \frac{1}{N} \log L(\theta)
\end{align}
この$L(\theta)$を尤度関数と呼びます。以上のことからKL情報量を小さくすることは、尤度関数の最大化すれば良いことになります。また、対数関数は単調増加関数であるため、尤度関数の最大化はその対数である$\log L(\theta)$の最大化とも取れるので、ボルツマンマシンの学習は、この対数尤度関数を最大化するように行うことにします。
その学習を行う方法の1つとして、勾配法が挙げられます。
勾配法では、対数尤度関数のパラメータ$\theta$、つまりバイアス$b_i$と重み$w_{ij}$に関する勾配を利用することで、以下のような更新式を得ることができます。
\begin{align}
b_i^{(t+1)} &= b_i^{(t)} + \epsilon \frac{\partial \log L(\theta)}{\partial b_i} \\
w_{ij}^{(t+1)} &= w_{ij}^{(t)} + \epsilon \frac{\partial \log L(\theta)}{\partial w_{ij}}
\end{align}
ここで、$\epsilon$は更新する量を調整するパラメータで、学習率と呼びます。
これでパラメータを更新するための式が求まりましたが、実はその勾配は以下のようにモデルパラメータに関する期待値の項(第2項目)が含まれます。
\begin{align}
\frac{\partial \log L(\theta)}{\partial b_i} &= \sum_{n=1}^{N} x_{ni} – N E_{\theta}[x_i] \\
\frac{\partial \log L(\theta)}{\partial w_{ij}} &= \sum_{n=1}^{N} x_{ni} x_{nj} – N E_{\theta}[x_i x_j]
\end{align}
この期待値を計算するためには、前述したボルツマンマシンの状態$\bf{x}$のすべての値の組み合わせの計算をしなくてはならず、ボルツマンマシンのノード数が増えると非常に時間がかかってしまうという問題があります。
そこで、MCMC(Markov Chain Monte Carlo)法などのサンプリング手法により、期待値計算を近似することで解決します。
サンプリング
サンプリングを行うことで、ある分布$p(x)$に従うサンプルを求めることができます。
以下に本論文で使用するサンプリング手法について簡単に説明します。
ギブスサンプリング
ギブスサンプリングはMCMC法の一つで、確率分布に従うように1つずつ値をサンプルすることを繰り返し、最終的に特定の分布に従ったサンプルを得る方法です。
はじめに、ノード$i$以外の全ノードの変数を並べたベクトルを$\textbf{x}_{-i}$と書き、条件付き分布$p(x_i|\textbf{x}_{-i}, \theta)$、つまり$\textbf{x}_{-i}$を指定したときの$x_i$の分布を考えます。これを式で表すと以下の様になります。
\begin{align}
p(x_i|\textbf{x}_{-i}, \theta) &= \frac{p(\textbf{x}, \theta)}{\sum_{\textbf{x}} p(\textbf{x}, \theta)} \\
&= \frac{\exp \left[\left(b_i + \sum_{j \in \mathcal{N}_i} w_{ij} x_j \right) x_i \right]}{1 + \exp \left( b_i + \sum_{j \in \mathcal{N}_i} w_{ij} x_j \right)}
\end{align}
ただし、$\mathcal{N}_i$はノード$i$と結合を持つノードの添字集合です。
このように各$x_i$の条件付き分布は求められるので、実際にサンプリングを行うときには、以下のように行います。
- $\textbf{x}_{-i}$が与えられたとき、上の式に従って$p(x_i | \textbf{x}_{-i}, \theta)$を計算する
- [0, 1]の一様乱数を生成し、この乱数値が計算した確率を下回れば$x_i = 1$、それ以外なら$x_i = 0$とする
ギブスサンプリングでは、この様に各$x_i$のサンプリングをすべてのノードに対して順番に繰り返すことで元の分布$p(\textbf{x}|\theta)$に従う$\textbf{x}$の値を計算できます。
ただし、サンプリング開始直後は確率分布に従っているとは言えないため、一定数のデータを破棄します。その数をburn-inと呼びます。また、サンプル同士を独立にするためにサンプリング間隔を開ける必要があります。今後これらのパラメータをそれぞれburn-in、サンプリング間隔と表記します。
D-Waveマシン
量子アニーリングは次式のハミルトニアンを最小化するような解を求める近似的なアルゴリズムです。
\begin{align}
H_0 = – \sum_{i} h_i \sigma_{i}^{z} – \sum_{i, j} J_{ij} \sigma_{i}^{z}\sigma_{j}^{z}
\end{align}
ここで、$\sigma_i^z$はパウリ行列のz成分です。
また、エネルギー関数の式と比較すると$h_i$がバイアス$b_i$に、$J_{ij}$が重み$w_{ij}$に対応していることがわかります。
そして、D-Waveマシンにより得られた解の分布がこのハミルトニアンをエネルギー関数としたときのボルツマン分布に従うことが実験的に知られているため、それを期待値計算に用います。
量子モンテカルロ法(QMC)
量子アニーリングは量子モンテカルロ法を用いることで古典コンピュータでシミュレートすることができます。
天下り的に示しますが、量子モンテカルロ法では以下のハミルトニアンを用います。
\begin{align}
H_c = – \frac{\beta}{m} \sum_l^m \left( \sum_i h_{i, l} x_{i, l} – \sum_{i, j} J_{ij, l} x_{i, l} x_{j, l} \right) – \frac{1}{2} \log \coth \left(\frac{\beta \Gamma}{m}\right) \sum_l^m \sum_i x_{i, l} x_{i, l+1}
\end{align}
ここで、$\beta$は逆温度、$m$はトロッター数を表します。
手順としては、はじめにトロッター数の数だけサンプリング対象(コピー)を用意します。そして、ある1つの対象に対してハミルトニアン$H_c$をエネルギー関数としたギブスサンプリングを行います。これをすべてのサンプリング対象について行うことを1ステップとして、繰り返します。繰り返しの際に徐々に横磁場の強さを弱めていくことで、解を収束の方向に導きます。
このようにして、エネルギー値の低い対象をサンプリング結果とするのが量子モンテカルロ法です。
先行研究の課題と本論文の目的
量子アニーリングの応用については最適化に関するものが多く、本論文のようにボルツマンマシンの学習に使用するような趣旨のものは少ないです。
その先行研究ではD-Waveマシンによるサンプリングを用いることで、ボルツマンマシンの性能評価の1つであるKL情報量が小さくなった、つまり性能が向上したと報告されています。
しかし、KL情報量は分布の近さを測ることはできますが、画像自体の評価をすることはできないのではないかというのが本論文の主張です。
手書き文字画像の分布を考えると、同じ数字の画像は分布間では近く、違う数字の画像間には境界が存在すると考えられます。ここで、5と6の境界に存在するサンプルを考えます。
もし、生成モデルがそのような画像を生成した場合、分布的には問題ないですが、数字の画像としては5と6の中間のような曖昧な場合、画像自体の評価は低くなると予想されます。
この様に、分布的には問題なくとも、画像の評価に直結しない場合があるため、画像自体を評価する方法が必要です。
では、どの様に評価をするのかというと、生成した画像を分類器によって直接的に評価します。この分類器はニューラルネットワークで実現され、ボルツマンマシンとは独立に学習をしておきます。
提案手法
ボルツマンマシンの学習
学習データとしては、MNIST(手書き数字画像)の5~9までの画像を用いて学習を行います。MNISTの元々の画像サイズは28×28ピクセルですが、D-Waveマシン上で扱うには大きすぎるため、8×6ピクセルにリサイズ処理をして学習データとします。
ボルツマンマシンの構造としては、全結合で53ノードのものを使用します。ただし、そのうち48ノードはデータを表すノードで、残りの5ノードはどの数字かを表すone-hot表現になっています。
つまり、6を生成する場合、その5ノードは(0, 1, 0, 0, 0)となり、8を生成する場合は(0, 0, 0, 1, 0)と、5ノードのうち特定のノードのみ1としてそれ以外を0とすることでどの数字かを操作します。
学習時に使用するサンプリング手法としては、ギブスサンプリングとD-Waveマシンによるものを使用し、比較を行います。
学習に関するパラメータを以下に示します。
| パラメータ | 値 |
|---|---|
| データ数 | 896 |
| バッチサイズ | 256 |
| エポック数 | 4000 |
| イテレーションあたりのサンプル数 | 200 |
| アニーリング時間 | 5 μs |
| 学習率 | 0.025 |
| L2ノルム正則化係数 | 1e-5 |
| モーメンタム係数 | 0.5 |
| D-Waveマシンのバージョン | 2000Q-5 |
評価方法
評価は前述したように事前に学習された分類器を用いて行います。
その分類器の構成を図1に示します。

この分類器において、以下の式で表される$R_a$を評価指標とします。
\begin{align}
R_a = \frac{D_m}{D_t}
\end{align}
ここで、$D_m$は特定の数字を生成したときに、その数字が分類器の判定した数字と一致した数、$D_t$は生成画像の総数です。これにより画像の品質をどの数字を表すかという指標で直接評価することができます。
評価時には、学習と同様のギブスサンプリング、D-Waveマシンによるサンプリングに加えて、D-Waveマシンから1000個のサンプルを取得し、その内エネルギー値の低い100サンプルを使用する方法も使用します。
これは、サンプリング結果から質の高いサンプルを使用することで、分散を抑える役割があります。なので、学習と評価時でのサンプリング手法の組み合わせは全6通りとなります。
ここまでの実験方法をまとめると図2のように表せます。
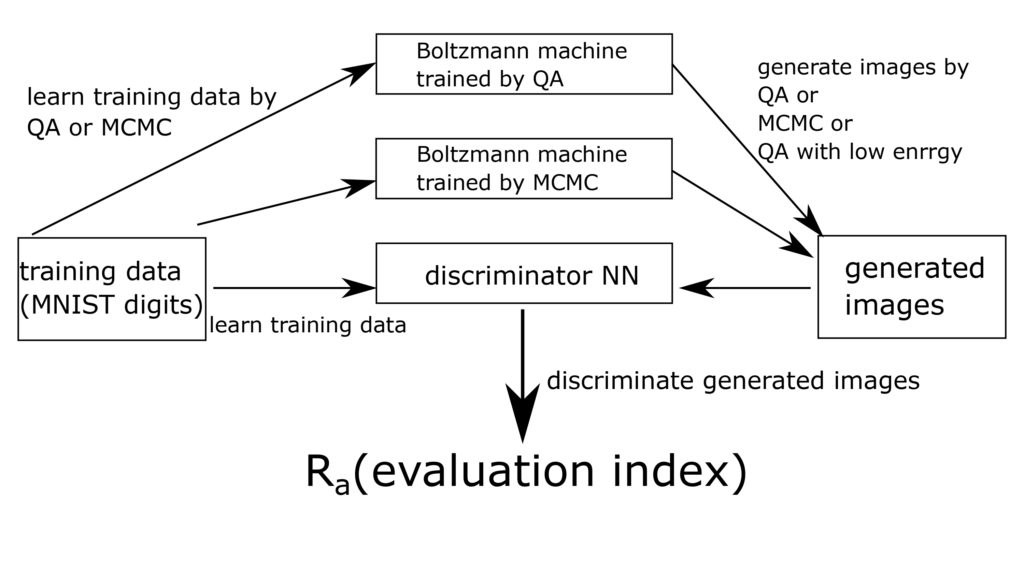
ここで、MCMCはギブスサンプリングで、QAがD-Waveマシンによるサンプリング、QA with low energyが上述したエネルギー値の低いものを用いるサンプリング手法です。また、discriminator NNが分類器を表しています。
実験結果
分類器の学習結果
はじめに、分類器を学習した結果について示します。
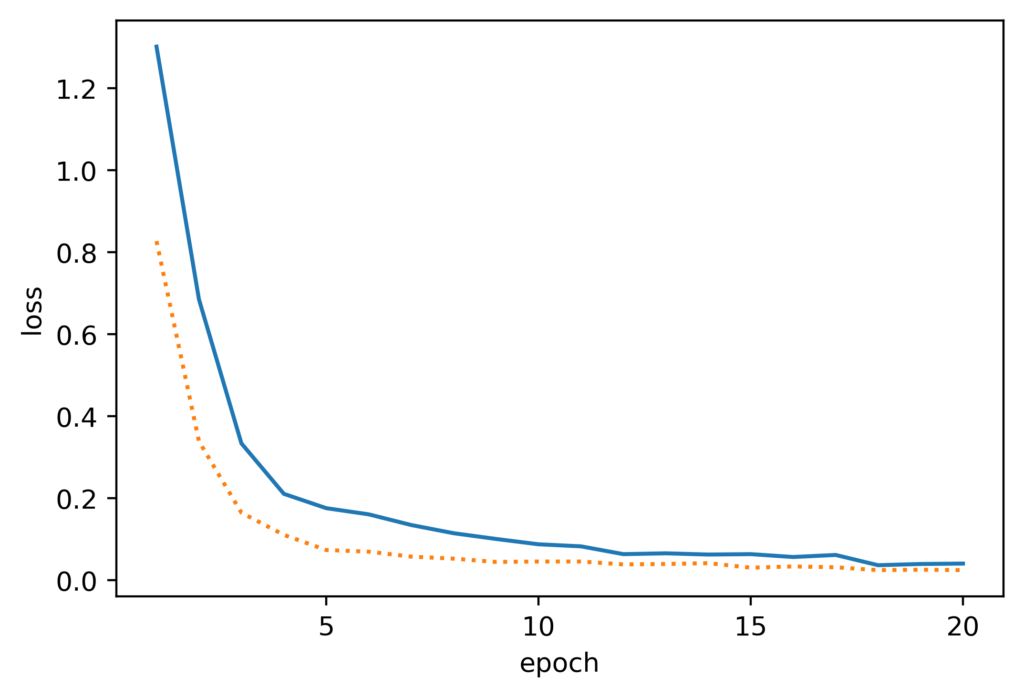
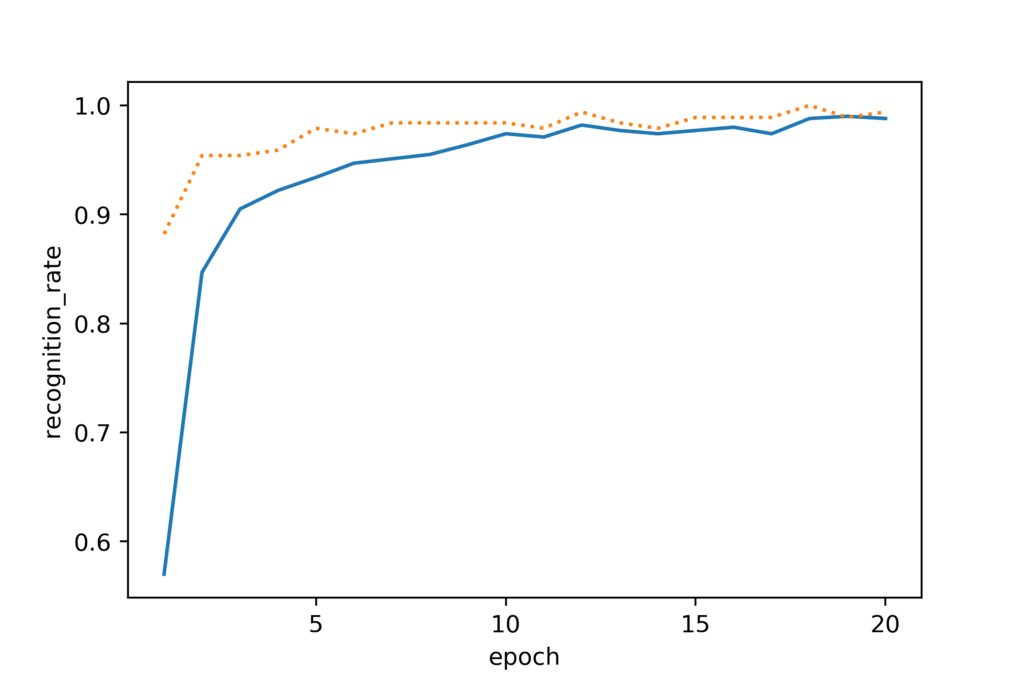
ここで、実線が訓練データ、波線が検証データに対するものになります。図3Aより、訓練誤差と検証誤差の差異が小さく汎化性能があることがわかります。また、図3Bを見ると検証データについて約98%程度の分類精度があるため、画像の評価に使用する上で十分な性能があるといえます。
ボルツマンマシンの学習・評価結果
各サンプリング手法の組み合わせに対しての評価指標$R_a$のエポック毎の推移を示します。
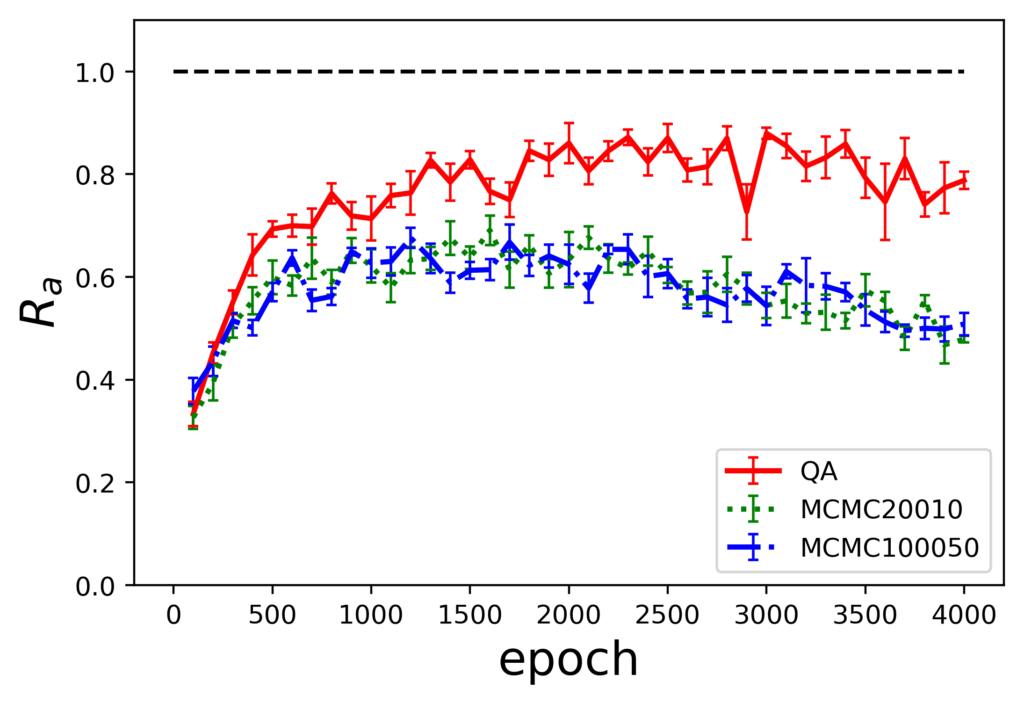
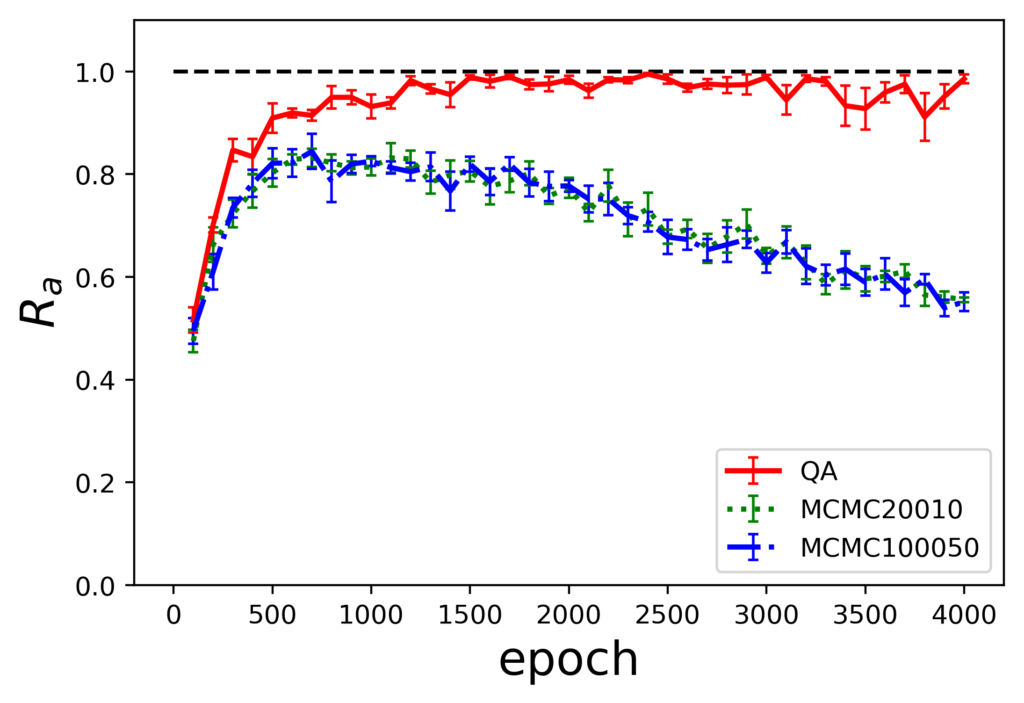
生成した場合の評価指標
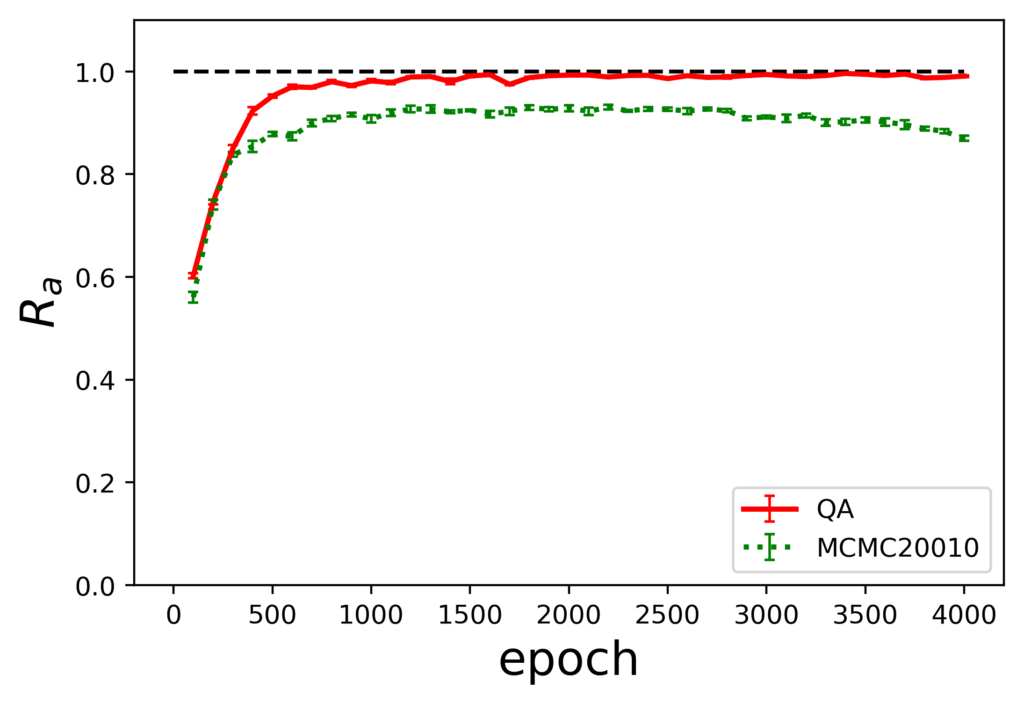
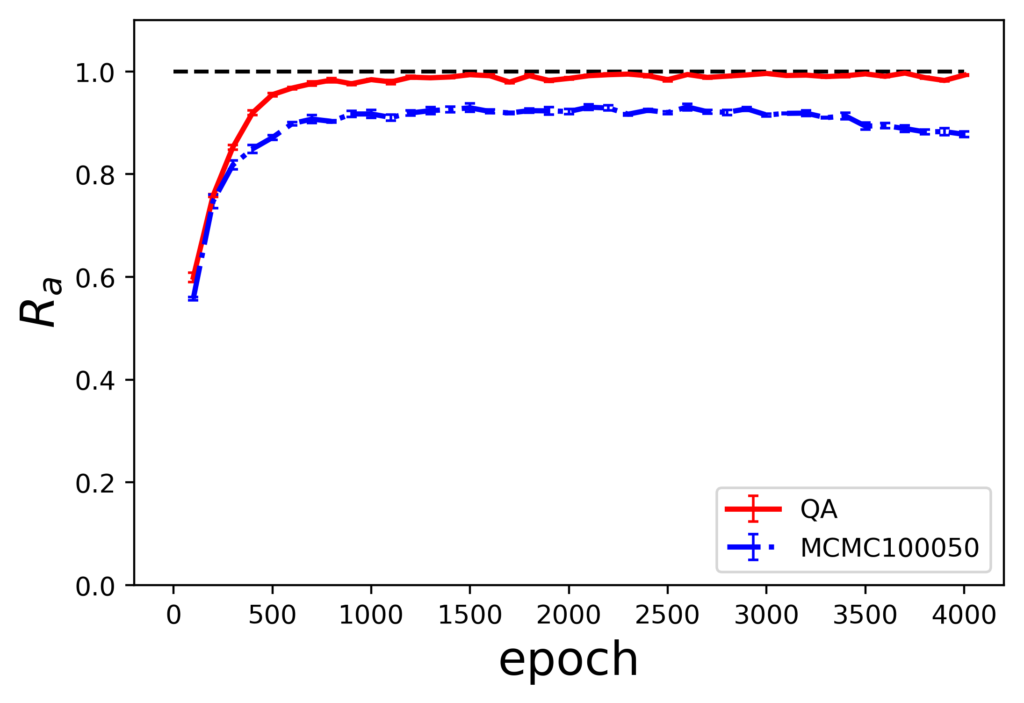
ここで、図の下の表記が生成時のサンプリング手法を示しており、表内の凡例に示されているのが訓練時のサンプリング手法になります。また、MCMCのあとの数値はギブスサンプリングを実行する際のパラメータであるburn-inとサンプリング間隔の値です。
結果から、訓練にMCMCを使用した場合は、QAを使用した場合に比べ10%程度評価指標の値が小さくなっています。また、訓練時MCMC、生成時QAの組み合わせでは過学習を起こしていることがわかります。
実際の生成結果として、QA with low energyで生成した結果を示します。ここで、色が付いている結果は分類器との結果が一致したものです。生成結果よりQAで学習したほうが品質は高いことがわかります。


ここまでの結果をまとめると以下の通りです。
- 生成時のサンプリング手法に限らず、QAを学習に用いた結果の方が優れている
- 生成時はMCMC法を用いた方が評価指標の値が安定しており、QAに対して高い値となっている
よって、学習にはQA、生成にはMCMCを用いた結果が良いということになります。
量子効果の検証
QAをボルツマンマシンの学習に用いることで過学習を抑えられ、性能が向上していることがわかりました。そこで、量子効果を検証するため、量子モンテカルロ法(QMC)による実験をします。
D-WaveマシンによるQAでは計算過程の横磁場が若干残った状態でボルツマン分布に従うとされています。そこで本来であれば横磁場の強さをサンプリングが進むに応じて弱め、最終的に0とすることで解を収束させるQMCですが、横磁場が残ることによる影響を調べるために横磁場を固定してQMCによる生成を行います。
ここで、横磁場の強さは量子モンテカルロ法の説明で出てきた式における$\Gamma$が対応しており、その値の変化に伴う評価指標の推移を観察します。
前節と同様にボルツマンマシンをQAとMCMC(1000, 50)で学習し、生成時には量子モンテカルロ法を用いて実験を行います。具体的には、横磁場の強度をgamma($\Gamma$) = 0.1、0.3、0.5、1.0と固定し、評価指標の値を観察します。
学習時のサンプリング手法ごとの評価指標の推移を以下に示します。
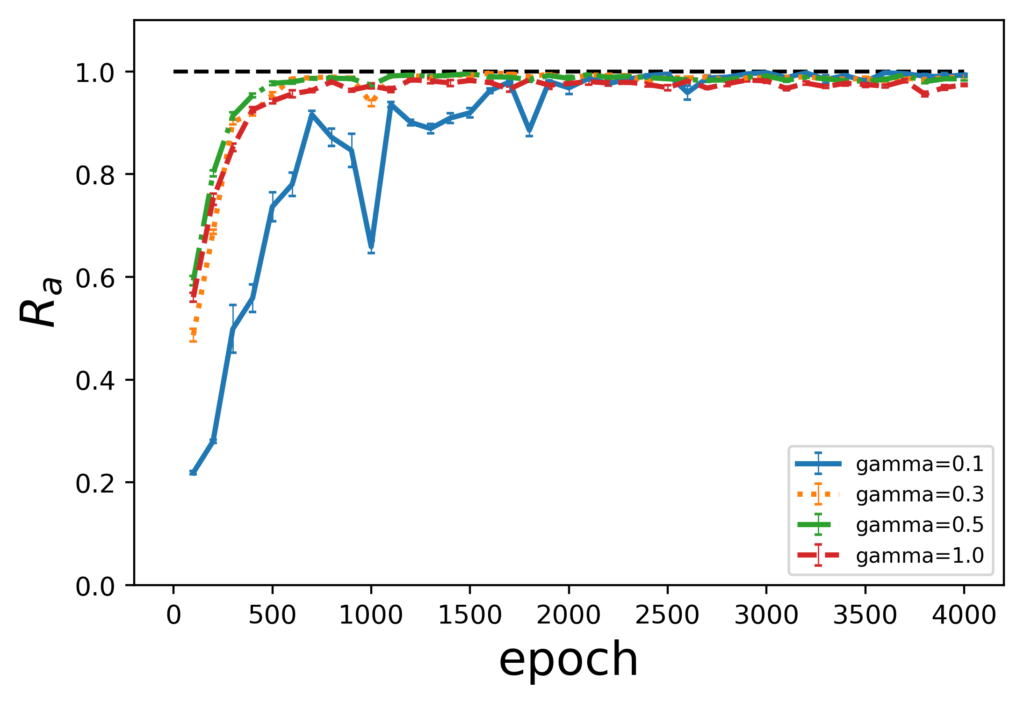
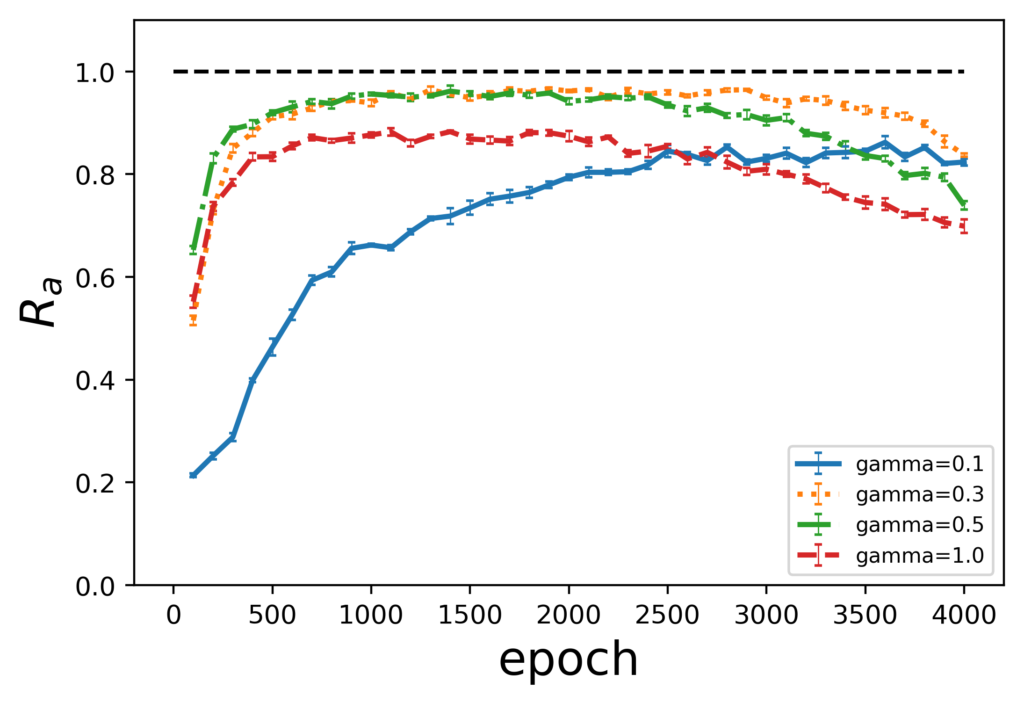
まず、学習時のサンプリング手法によって、横磁場の影響が異なっていることが見て取れます。QAで学習した場合では、横磁場の影響に限らず評価指標の値は1.0付近に収束していますが、gamma=0.3以上のグラフの方が安定しています。一方で、MCMCで学習した場合では、gamma=0.3以上で過学習を起こしており、終盤は評価指標の値が減少しています。このことから、性能向上のためには横磁場を適度にかける必要があると言えます。
また、前節のD-Waveマシンで生成した結果と比べ評価指標の値が向上していることがわかります。これは、量子モンテカルロ法にはないD-Waveマシン自体の要因などにより、性能が下がってしまうことを示しています。
結論
QAで学習したボルツマンマシンの生成結果は、古典手法(MCMC)で学習したものと比較して、品質の高い画像を生成できていることが確認できました。
学習においては、QAを用いることでモデルの過学習を抑えることができ、性能向上を図ることができることがわかりました。
また、横磁場の影響を検証することで、適度な横磁場が性能向上に寄与していることがわかりました。
参考文献
[1] 深層学習, 岡谷貴之, 2015
あとがき
本論文を解説することで、ボルツマンマシンを用いた機械学習について理解を深めるとともに、QAを絡めた手法についても勉強することができました。
論文内では、MCMCと比較して、QAが優れていることは結果からわかりましたが、KL情報量の指標と今回の分類器を用いた指標の定量的な比較がなかったことが少し残念でした。
ただ、QAを最適化目的ではなくサンプリングとして用いることで生成モデルを実現するという点は面白かったため、最適化問題以外のQAの利用についても調べてみたいと思いました。